Depth First Search

What is Depth First Search?

Works by going "deeper" into one part of the graph and visiting all of its nodes all the way to the end.

• once it has no further nodes to visit for that sub-tree
• it backtracks to the latest point where it could make a different choice
• then explores out from there
• usually done in a left to right order
  • evaluates the left-most branch/sub-tree of the tree
  • then it proceeds to the one to the right of it
  • ... and so on until all the branches are visited

Depth First Search Traversals

• pre-order: root -> left -> right
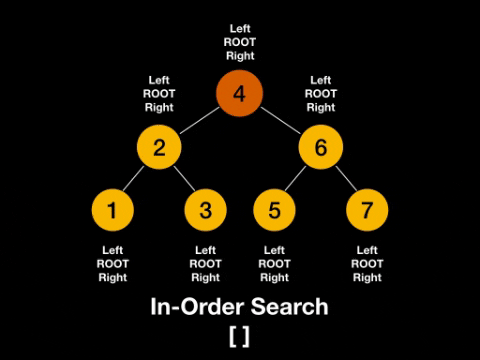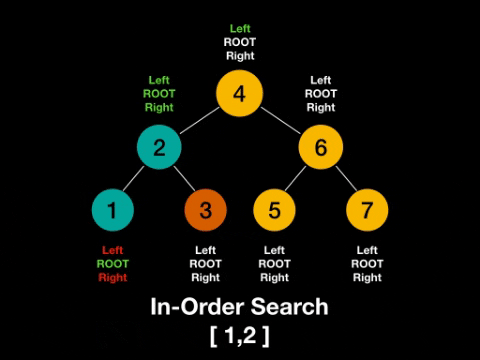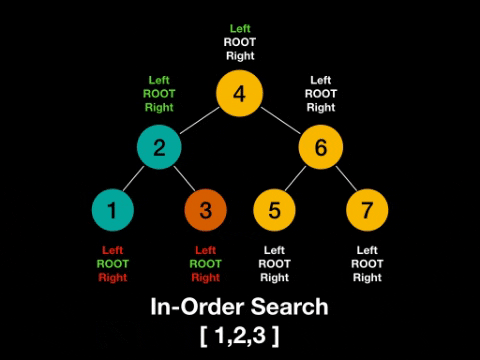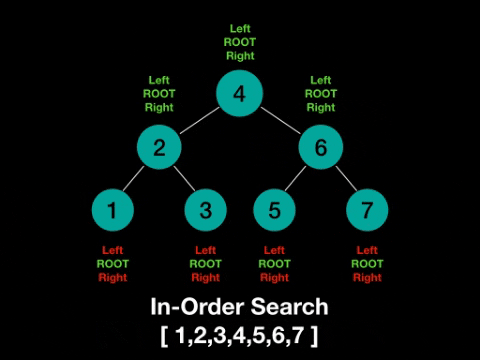
• in-order: left -> root -> right
• post-order: left -> right -> root

*Think about the pre/post/in being the location of ROOT

Pre-Order: root -> left -> right

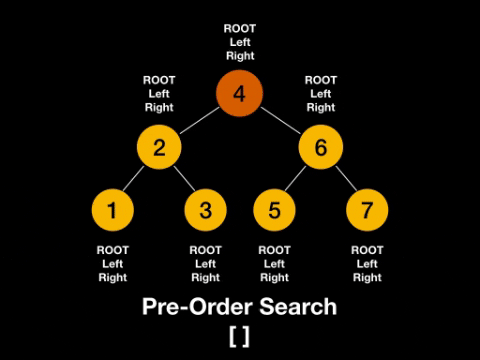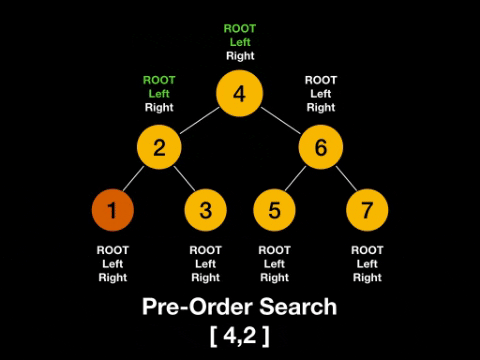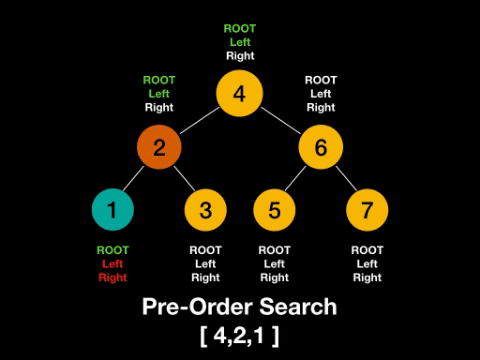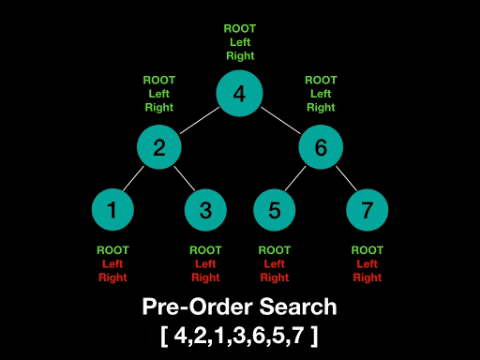
In-Order: left -> root -> right

Post-Order: left -> right -> root

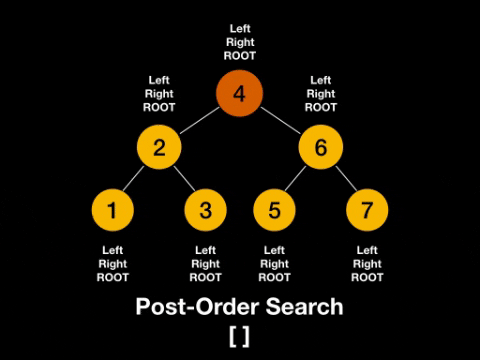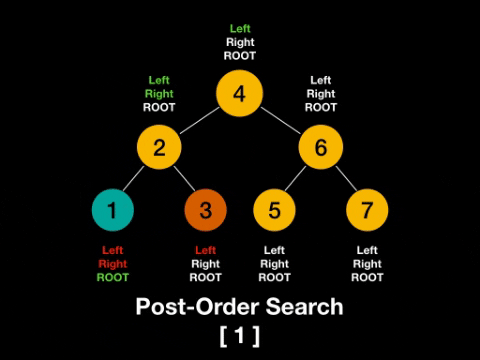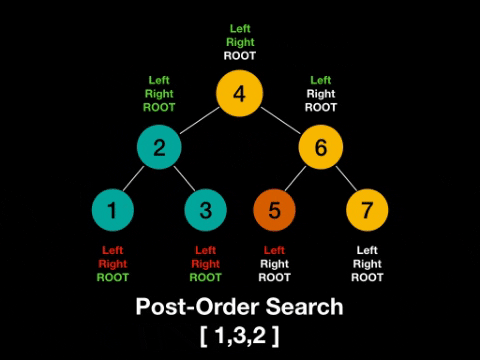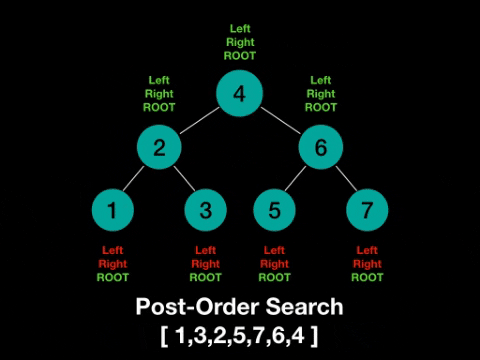
Javascript Depth First Search

// Binaary Tree Constructor Function
function BST(value) {
  this.value = value;
  this.left = null;
  this.right = null;
}
//...//
BST.prototype.depthFirstTraversal = function (iteratorFunc, order) {
  // pre-order will iterate over parent node before child
  if (order === 'pre-order') {
    iteratorFunc(this.value);
  }

  if (this.left) {
    // if left node exists, run depthFirstTraversal on it
    this.left.depthFirstTraversal(iteratorFunc, order);
  }

  // in-order will run iteratorFunc on parent node after left child
  if (order === 'in-order') {
    iteratorFunc(this.value);
  }

  if (this.right) {
    // if right node exists, run depthFirstTraversal on it
    this.right.depthFirstTraversal(iteratorFunc, order);
  }

  // post-oder will run iteratorFunc on parent node after both children
  if (order === 'post-order') {
    iteratorFunc(this.value);
  }
};

// example simple iteratorFunc
function log(value) {
  console.log(value);
}

var bst = new BST(50);
//...//
bst.depthFirstTraversal(log);

Use Cases for Depth First Search

TODO: consolidate and simplify all of that mess below....

• Find Solutions for Puzzles
  • games like chess, sudoku,
    • board configurations are often represented in the form of a game tree
    • variations of DFS are used for finding the shortest or most optimum set of moves
• Find Connected Components
  • You can use DFS to find connected components in an Undirected Graph
• Find Strongly Connected Components
  • DFS has applications in a social graph as well
    • you want to suggest or advertise certain content specific to people who have liked similar pages or liked similar videos
    • could be represented as a strongly connected graph
      • that uses DFS to search for entities that are similar to each other
  • Vehicle Routing Problem
    • finding the optimal (Minimize total cost routes) for multiple vehicles visiting a set of locations
• Finding a Path
  • It can be used to see if a path exists from vertex u to vertex v.
• Topological Sorting Algorithm
  • Directed Acyclic Graphs (DAG) can be used to maintain linear ordering of tasks
  • For instance
    • vertices of graph may represent tasks to be performed
    • edges may represent constraints that one task must be performed before another
  • ATM Example:
    • In an ATM transaction, tasks happen in a certain sequence
    • insert ATM... enter PIN... withdraw money
    • you can’t withdraw money before you insert/scan a card
  • This order of operations can be represented using a DAG, where you could use topological sorting
  • Turn-based games like chess use game trees
    • certain moves become available only when the player reaches a certain board config